Доверительная вероятность представляет собой статистический показатель, характеризующий надежность оценки параметров генеральной совокупности на основе выборочных данных. Рассмотрим методы ее определения.
Содержание
Основные понятия
| Термин | Определение |
| Доверительная вероятность | Вероятность, с которой доверительный интервал содержит истинное значение параметра |
| Доверительный интервал | Диапазон значений, содержащий оцениваемый параметр с заданной вероятностью |
| Уровень значимости | Вероятность ошибки первого рода (α = 1 - доверительная вероятность) |
Методы определения доверительной вероятности
Для среднего значения при известном σ
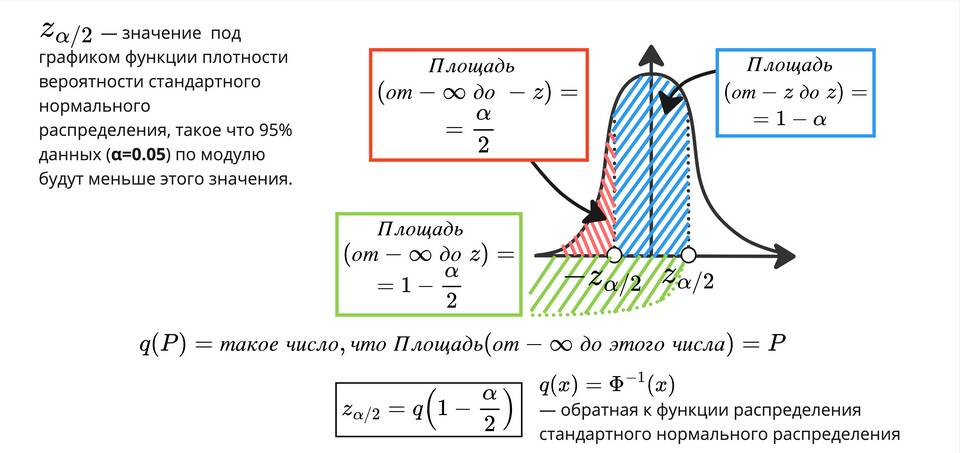
- Выберите уровень доверия (90%, 95%, 99%)
- Определите соответствующее значение z-критерия
- Рассчитайте стандартную ошибку: SE = σ/√n
- Вычислите доверительный интервал: x̄ ± z*SE
Для среднего значения при неизвестном σ
- Используйте t-распределение Стьюдента
- Определите степень свободы: df = n-1
- Найдите критическое значение t-критерия
- Рассчитайте доверительный интервал: x̄ ± t*(s/√n)
Факторы, влияющие на доверительную вероятность
| Фактор | Влияние |
| Объем выборки | Увеличение n уменьшает ширину интервала |
| Разброс данных | Большая дисперсия увеличивает интервал |
| Выбранный уровень доверия | Высокая вероятность дает широкий интервал |
Для доли признака
- Рассчитайте выборочную долю: p̂ = x/n
- Определите стандартную ошибку: SE = √(p̂(1-p̂)/n)
- Выберите z-значение для нужного уровня доверия
- Вычислите интервал: p̂ ± z*SE
Практические рекомендации
- Для большинства исследований используют 95% доверительную вероятность
- При малых выборках (n<30) применяйте t-распределение
- Проверяйте выполнение условий нормальности распределения
- Для пропорций используйте поправку на непрерывность при малых n
Важные замечания
- Доверительная вероятность не равна вероятности того, что параметр лежит в интервале
- Метод построения зависит от типа оцениваемого параметра
- Для непараметрических данных используйте бутстреп-методы
- Всегда указывайте использованный уровень доверия в отчетах