В евклидовой геометрии сумма внутренних углов любого треугольника всегда постоянна и не зависит от его вида или размеров. Это фундаментальное свойство было доказано еще в древнегреческой математике.
Содержание
Основное свойство треугольников
В евклидовой геометрии сумма внутренних углов любого треугольника всегда постоянна и не зависит от его вида или размеров. Это фундаментальное свойство было доказано еще в древнегреческой математике.
Теорема о сумме углов треугольника
Сумма внутренних углов любого треугольника равна 180 градусам (или π радианам). Это утверждение справедливо для:
- Остроугольных треугольников
- Тупоугольных треугольников
- Прямоугольных треугольников
Частный случай: прямоугольный треугольник
| Угол | Величина |
| Прямой угол | 90° |
| Два острых угла | α и β, где α + β = 90° |
| Сумма всех углов | 90° + α + β = 180° |
Доказательство для прямоугольного треугольника
- Рассмотрим прямоугольный треугольник ABC с прямым углом C
- Проведем высоту CD к гипотенузе AB
- Образовались два подобных треугольника ADC и BDC
- Углы при основании этих треугольников равны острым углам исходного
- Сумма углов в каждом из них составляет 180°
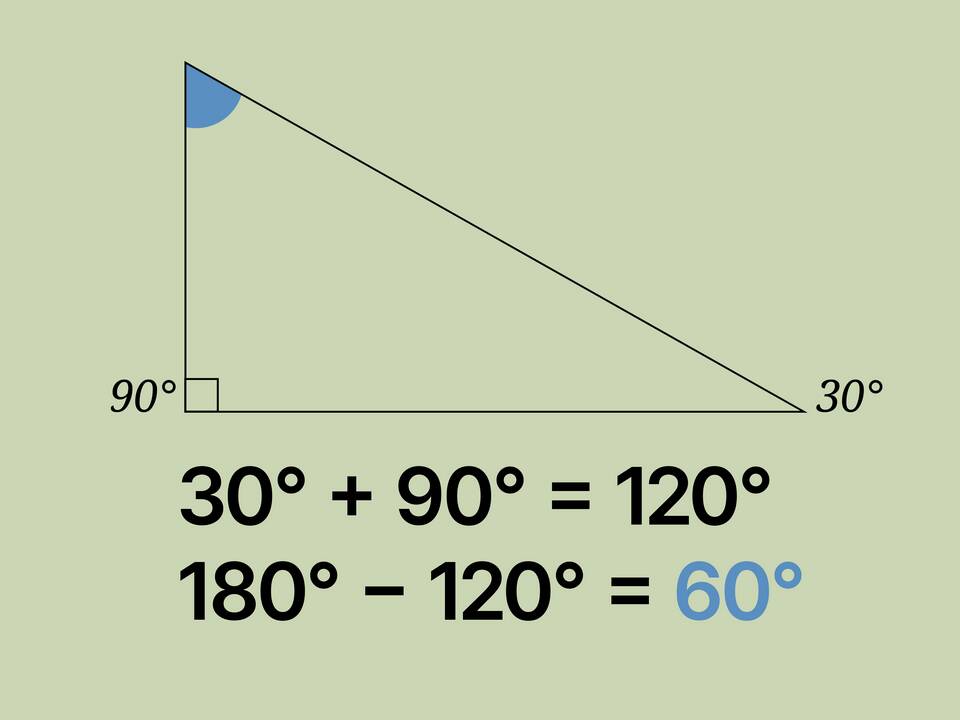
Пример расчета
Для треугольника с углами 90°, 30° и x:
- 90° + 30° + x = 180°
- x = 180° - 120° = 60°
- Таким образом, сумма острых углов: 30° + 60° = 90°
Практическое применение
| Область | Использование |
| Геодезия | Расчет расстояний и углов |
| Строительство | Проектирование конструкций |
| Навигация | Определение курса |
Важное следствие
В прямоугольном треугольнике сумма острых углов всегда равна 90 градусам. Это свойство часто используется при решении геометрических задач и доказательстве теорем.
